I
我们在第二章已看到,不可逆过程描述了形成非平衡耗散结构的自然之基本特征。这样的过程在经典力学和量子力学的时间可逆定律所支配的世界里是不可能的。耗散结构需要时间之矢。而且,若想用这些定律引入的近似来解释耗散结构的出现是没有希望的。
我始终坚信,认识耗散结构乃至更一般地认识复杂性的动力学起源,是当代科学最引人入胜的概念难题之一。如第一章所述,对于不稳定系统,我们必须在统计层次上表述动力学定律。这剧烈改变了我们对自然的描述。在这种表述中,物理学基本客体不再是轨道或波函数,而是概率。因此,我们到了18世纪物理学领域之外的“概率革命”的尾声。然而,面对这种激进结论的含意,为了得到不太极端的解答,我踌躇良久。在《从存在到演化》一书中,我写道:“在量子力学中,有些观测量的数值不能够被同时确定,即坐标和动量。(这是海森伯不确定度关系和玻尔互补原理的精髓。)在此,我们也有一个互补性——动力学描述与热力学描述之间的互补性。”这可能是解决与不可逆性联系在一起的概念难题的一个更不极端的方法。
回顾过去,我对我早先著作中的这段叙述感到遗憾。如果存在一个以上的描述,那么谁来选择正确的描述呢?时间之矢的存在并没有带来方便,它是由观测强加的一件事实。然而,最近几年我们对不稳定系统动力学的研究结果,迫使我们在统计层次上重新表述动力学,并断言这一表述导致经典力学和量子力学的扩展。在本章,我将描述涉及到的某些步骤。
近100年来,我们已经知道,甚至简单的概率性过程也有时间方向。在第一章我们已经提到过“无规行走”,另一个例子是由埃伦费斯特(Paul
Ethenfest)和埃伦费斯特(TatianaEhrenfest)提出的“瓮模型”(见图3.1)。
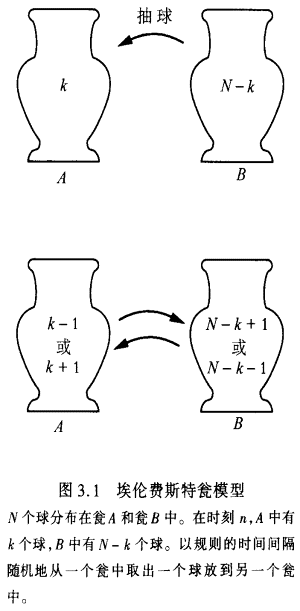
假设在瓮A和瓮B中分布有N个物体(例如球),以规则的时间间隔(例如每秒)随机地选取一个球,从一个瓮移到另一个瓮中。设在时刻n,A里有k个球,故B里有N-k个球。则在时刻n+l,A里有k-l个球或者k+1个球。这些是明确定义的转移概率。让我们继续进行这场游戏。我们预计,作为球交换的结果,我们将达到每个瓮中约有N/2个球的情况。但是,涨落将不断出现。我们甚至有可能返回到时刻n时瓮A中再次有k个球的情况。正是在概率分布层次上我们看到趋于平衡的不可逆趋向。无论起点如何,可以证明,经n次转移后在一个瓮中找到
k个球的概率pn(k),当n→∞时趋于二项分布N!/(k!(N-k)!)。这一表达式有k=N/2的最大值,而且考虑了分布中的涨落。在玻尔兹曼模型中,最大熵恰好对应于这个二项分布。
埃伦费斯特模型是“马尔可夫过程”(或叫“马尔可夫链”)的一个范例,是以俄国大数学家马尔可夫(Andrei
Markov)的名字命名的,他最先描述了此种过程。一旦我们有了概率描述,就常常能够导出不可逆性。但我们如何将概率性过程与动力学联系起来呢?这仍是根本性的难题。
我们已经看到,统计物理学或群体物理学的先驱们已经在这一方向上迈出了基本的一步。麦克斯韦、玻尔兹曼、吉布斯和爱因斯坦都强调过由概率分布ρ描述的系综的作用。那么,一个重要问题是,一旦达到平衡,这一分布函数的形式是什么?设q1,…,q2和p1,…,Ps分别为构成该系统的粒子的坐标和动量。在第一章,相空间由坐标和动量来定义。我们还引入了概率分布ρ(q,p,t)(参见第一章第Ill节)。现在,我们将用单个字母q表示所有坐标,用单个字母p表示所有动量。当ρ变成与时间无关时,达到平衡。所有教科书中都证明,当ρ只依赖于总能量时,才能发生这种情况。第一章第III节提到,总能量是动能(粒子的运动所致)与势能(粒子间的相互作用所致)之和。当用q和p表达时,总能量叫做哈密顿量H(p,q),它随时间保持不变。这就是能量守恒原理,即热力学第一定律。所以,在平衡时,ρ是哈密顿量H的函数是很自然的。
一个重要的特例,是所有系统都具有相同能量E的系综。在整个相空间,除分布函数为常量的表面H(p,q)=E外,其余任何地方分布函数均为零。这叫做“微正则系综”。吉布斯证明,这样的系综确实满足平衡热力学定律。他还考察了其他系综,如所有系统都与处于温度T的热库发生相互作用的“正则系综”。这导致了分布函数指数地依赖于哈密顿量,ρ现在正比于exp(-H/kT),其中T是热库的温度,k是玻尔兹曼常量(该常量使得指数成为量纲一的量)。
一旦平衡分布给定,我们就可以计算所有的热力学平衡性质,诸如,压强、比热等。我们甚至可以超出宏观热力学,因为我们能够包括涨落。一般认为,在平衡统计热力学的广泛领域里不存在什么遗留的概念困难,只存在大部分可以用数值模拟来解决的计算困难。系综理论应用于平衡情形无疑十分成功。请注意:吉布斯所作的平衡热力学的动力学诠释是借助系综,而不是轨道。为了包含不可逆性,我们必须扩展这一方法。
根据经典物理学和量子物理学,在轨道层次(或波函数层次)不存在时间建序,因为未来和过去扮演着相同的角色,这十分自然。然而,在统计描述的层次上用分布函数会发生什么情况呢?我们来观察一杯水。在这个玻璃杯中有数目庞大的分子(1023数量级)。从动力学观点来看,正如第一章所定义的,这是一个不可积庞加莱系统,因为存在着我们无法消除的分子间相互作用。我们可以把这些相互作用现为分子间的碰撞(在第五章,我们将更精确地定义“碰撞”这一术语),并且用统计系综
ρ来描述包含大量碰撞的水。水在变老吗?如果我们只考虑单个的水分子,它们在地质时间尺度是稳定的,水肯定没有变老。然而从统计描述的观点来看,在此系统中存在着自然时间秩序。老化是群体的属性,恰如生物进化的达尔文理论中的情况。它是趋于平衡分布的统计分布,如上面定义的正则分布。要描述这种向平衡的趋近,我们需要关联概念。
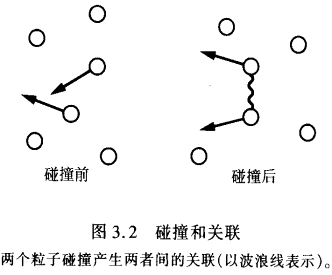
考虑依赖于两个变量x1和x2的概率分布ρ(x1,x2)。若x1和X2彼此无关,则我们有因式分解ρ(x1,x2)=ρ1(x1)ρ2(x2)。于是,概率ρ(x1,x2)是两个概率之积。反之,若ρ(x1,x2)不能分解因子,则意味着x1与x2关联。现在我们回到那杯水中的分子。水分子之间的碰撞有两个效应,一是使速度分布更对称,二是产生关联(见图3.2)。但两个关联的粒子还会与第三个粒子碰撞,于是二粒子关联转换为三粒子关联,如此等等(参见图3.3)。
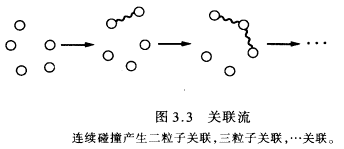
我们现在得到一个以时间为序的关联流。对这一关联流很有价值和激起争论的类比就是人的交流。两个人相遇交谈,从而在某种程度上修改他们的看法。这些修改带给随后的相遇,又进一步修改观点。这一现象叫传播。社会中存在交流流,好比物质中存在关联流。当然,我们也可以想象逆过程通过破坏关联使速度分布不那么对称(见图3.4)。
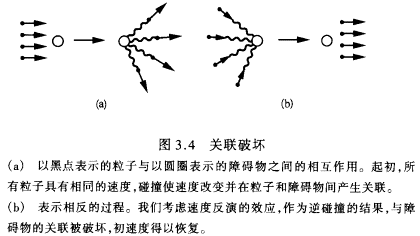
因此,我们需要一个随着时间的推移使速度分布更加对称的过程行将有效的因素。我们将看到,这恰恰是庞加莱共振的作用。我们现在开始瞥见包含不可逆性的统计描述,它将是导出平衡分布的关联动力学。
图3.3所示依时间为序的关联流的存在,已由计算机模拟得到证实。我们也可以再现通过时间反演(其中我们反演粒子的速度)产生如图3.4所示的过程。但我们只能对短期时间和有限数目的粒子实现这种反演关联流,此后,我们重新具有包括使系统趋于平衡的数目越来越大的粒子的关联流。
在统计层次上给出不可逆性的意义的这些结果,在将近30年前就已经得到,但目前仍有一些基本问题有待解决。如何在统计描述层次产生不可逆性,而不在我们借助轨道来描述动力学的时候产生不可逆性?这是否是我们的近似所引起的?而且,(例如在计算机实验里)我们观察到的渐次关联,也许是计算机时间限制所引起的?显然,通过碰撞制备产生关联的不关联粒子,比制备能够导致其中的关联被破坏的系综,所需程序要短。
但是,为什么要从概率分布入手?概率分布描述轨道丛或系综的性态。我们采用系综到底是因为我们“无知”,还是像第一章讨论的那样隐含有更深刻的原因?对于不稳定系统,系综与个体轨道相比确实显示出新的特性。这就是我们现在将用若干简单例子加以说明的东西。
II
在本小节里,我们将关注确定性混沌,以及一种特别简单类型的混沌二者都对应于混沌映射。与在普通动力学中发生的情况相反,映射中的时间仅以离散间隔起作用,比如在第I节中我们讨论过的埃伦费斯特瓮模型。因此,映射表示动力学的简化形式,它使我们比较容易把个体描述层次(轨道)与统计描述进行比较。我们将考察两种映射。第一个例子描绘简单周期性态;第二个例子描绘确定性混沌。
在第一个例子里,我们考虑“运动工程”xn+1=xn+
1/2(mod l)。mod 1的意思是,我们只处理0和1之间的数。经过两次推移后,我们回到初始点(即x0=1/4,x1=3/4,x2=3/4+2/4=5/4=1/4)。这种情况如图3.5所示。
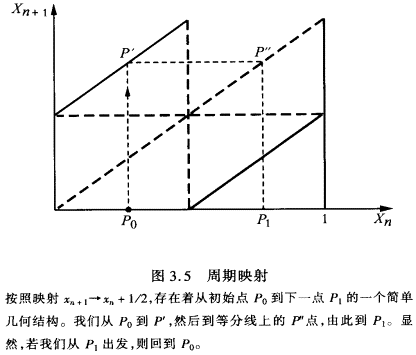
不考虑由轨道定位的单个的点,而考虑由概率分布ρ(x)描述的系综,是很有意义的。轨道对应于系综的特殊集合,其中,坐标X取明确定义的值Xn,分布函数ρ则退化成单个点。第一章第III节曾提到,这可以写为ρn(x)=δ(x-xn)。(δ函数是除了x=xn外其余所有值皆为零的一种函数的符号。)用分布函数ρ,映射可以表达成ρn+1(x)与ρn(x)之间的关系。故我们可以写成ρn+1(x)=Uρn(x)。形式上,ρn+1通过作用于ρn(x)上的算符U而得到。这个算符称为佩龙一弗罗贝尼乌斯算符。在这一点上,它的显式对我们并不重要,但值得注意的是,并没有在U的结构中引人新的元素(运动方程除外)。显然,系综描述必须把轨道描述作为一种特例,因而我们有δ(
x-xn+1)=Uδ(x-xn)。这只不过是将运动方程重写的一种方法,因为,推移一次后,Xn就变成了Xn+1。然而,主要问题在于:这是唯一的解,还是作为由不能用轨道表达的佩龙-弗罗贝尼乌斯算符所描述的系综演化的新解?在我们周期映射的例子中,回答是否定的。对于稳定系统,个体轨道与系综的性态之间没有任何差别。对于不稳定动力学系统,正是个体观点(对应于轨道或波函数)与统计观点(对应于系综)之间的这一等价性被打破了。
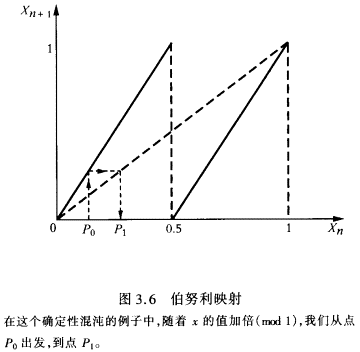
混沌映射最简单的例子是伯努利映射。这里,我们把0和1间的数值每一步都乘以2,得到运动方程:xn+1=2xn
(mod 1)。这个映射如图3.6所示。运动方程再次成为确定性的,一旦我们已知xn,则xn+1的数值也就确定了。这里我们有一个确定性混沌的例子,之所以如此称呼,是因为如果我们用数值模拟来跟踪轨道,就会发现轨道是无常的。因为坐标x在每一步都乘以2,两条轨道之间的距离将为(2n)=exp(nln2),仍然是mod
1。用连续时间t,这可以写成exp(t λ),其中λ=ln2,λ称为李雅普诺夫指数。这表明,轨道指数地发散。这种发散就是确定性混沌的标志。若我们等待足够长的时间,则轨道最终将趋近0与1之间任意选择的任何点(参见图3.7)。这里,我们有一个导出随机性的动力学过程。过去,确定性宇宙中的这一表现流被许多大数学家反复研究过,诸如克罗内克(Leopold
Kronecker(1884))和外尔(Hermann Weyl(1916))。按照普拉托(Jan
von Plato)的说法,类似的结果早在中世纪就已得到,所以,这肯定不是一个新问题。然而新鲜之处在于,把随机性与算符理论联系起来的伯努利映射的统计表述。
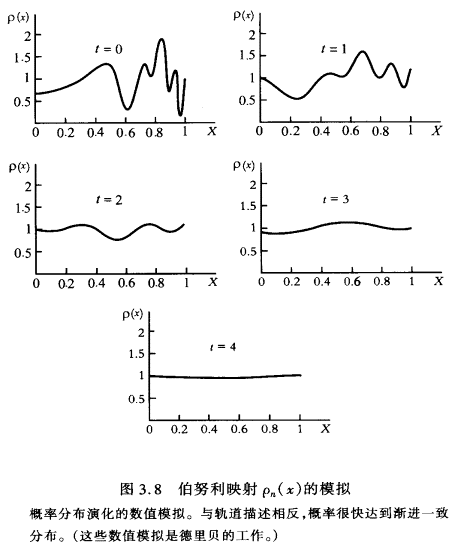
我们现在转向用佩龙-弗罗贝尼乌斯算符的统计描述上来。在图3.8中,我们看到算符U对分布函数的影响。轨道描述的差异是显著的,因为分布函数ρ(x)很快变为常量。因此,我们断言,用轨道描述的一方与用系综描述的另一方之间的基本差异必然存在。总之,轨道层次上的不稳定性导致统计描述层次上的稳定性。
这如何可能呢?佩龙-弗罗贝尼乌斯算符仍允许轨道描述δ(x-xn+1)=Uδ(x-xn),但意料之外的特点是,它还允许只适用于统计系综而不适用于个体轨道的新解。个体观点与统计描述之间的等价性被打破了。
这件令人震惊的事实揭开了数学和理论物理学的新篇章。虽然混沌问题不能在个体轨道层次上加以解决,但它能在系综层次上得到解决。我们现在可以谈论混沌定律。我们将在第四章里看到,我们甚至可以预言分布ρ趋向平衡的速率(对于伯努利映射它是常量),并建立这一速率与李雅普诺夫指数之间的关系。
我们怎么理解个体描述与统计描述之间的差异呢?在第四章,我们将更详细地分析这一情况。我们将看到,这些新解需要分布函数光滑,这就是为什么此种新解不适用于个体轨道的原因。用δ(x-xn)表示的轨道不是光滑函数,因为它当且仅当x=xn时不为零,当x≠Xn时为零。
因此,用分布函数的描述比从个体轨道导出的描述更加丰富,这和我们在第一章第III节所得出的结论一致。对于不稳定映射,轨道仅是佩龙-弗罗贝尼乌斯方程的特解。这也适用于具有庞加莱共振的系统(参见第五、第六章)。就概率分布而言,有时间方向的关联流是这些新解中的要素,而无时间方向的过程存在于个体轨道层次。
我们方法根本性的妙招,是打破个体描述与统计描述之间的等价性。下一章我们将更详细地讨论在统计层次出现于混沌映射中的新解。
我们现在发现自己所处的情况令人联想起我们在热力学中遇到的情况(见第二章)。平衡热力学的异常成功,妨碍了其中出现耗散结构和自组织的非平衡情形中物质的新属性的发现。类似地,经典轨道理论和量子力学的成功,阻碍了动力学向统计层次的扩展,阻碍了把不可逆性结合到对自然的基本描述之中。
|