|
要想知道厂商是如何选择投入和产出、制定价格和进行其他决定市场结构的活动的，就要分析企业行为。首先我们考察生产是什么，然后试图回答为什么存在厂商问题，接下来分析限制厂商规模的因素，并努力弄清每个厂商面对的成本。利润最大化模型占了很大篇幅，然后我们提出可供选择的厂商动机理论。
生产的定义
我们可以把生产定义为在一定时间和（或）空间中，使用任何资源将一种商品转变为另一种商品。因此，从广义上说，生产不仅包括制造，也包括仓储、批发、运输、零售、再包装，甚至包括想要改变管制机构的法规、雇佣律师和会计师来寻找税收漏洞等等。
生产既包括货物，也包括服务，因为“商品”一词与两者都有关。但是，在以下几页中，我们将只考察货物的生产，以简化分析。服务，像洗涤、修理等等也可以以同样的方式来把握。
生产是一个流量概念。这种活动是用单位时间产出率来度量的，其中产出是以质量既定的计量单位来表达的。因此，当我们讲到增加生产的，我们指的是增加产出率，而生产的所有其他方面保持不变。
为什么存在厂商
商品是由厂商生产的。在开始时我们把厂商（生产单位）的定义限于任何有1个雇主和1个或1个以上雇员的合法组织。支付给雇员的是合同工资，雇员在单位时间中取得的合同工资与产出率和销售率无关。另一方面，雇主（它也定义为企业家——组织者和风险承担者）并未获得合同工资率。相反，在支付了所有合同工资之后如果还有剩余，那么业主获得的就是剩余部分的收益。在会计上，每年收益中剩余下来的称为利润，或净收入。经济学也称之为剩余或净收益。
为什么存在厂商？理论上，个人也可以——比方说——制造汽车。但事实上绝大多数汽车是汽车厂商生产出来的。生产称为汽车的最终产品的许多活动是在一个汽车制造商内部进行的。
只要合作或联合体努力生产的产品多于各个孤立生产者生产的产品总和，就会有厂商存在。当然，这个差额必须至少与组织、监督、计量和实施与雇员所订合同等所费成本减去与每个独立剩余索取者相互订合同所需交易费用的差额一样大。
许多人可以从经验中认识到，厂商的存在不过是承认经济交易不是没有费用的。双方彼此间的交换包括提出要求的费用、商谈的费用、接受合同的费用、交货的费用、检查费用、担保费用和其他从事与物品和服务交换有关活动的费用。它们一般称为交易费用。由于存在着交易费用，因此，取消某种市场交易，代之以组织内部的交易，用这种方式组织生产可能较便宜。它是由既是生产过程的监督者，又是生产过程的指导者的企业家来支配的。
但是，这种组织的确也有缺点。由不索取任何剩余的个人组成的团体来进行生产增加了监督、计量、指导和续订合同的费用。若10个海地篮子编织者作为个人实体分别生产，即每个人都是企业家的话，则每个编篮人都会充分感受到“不干活”的压力。每个懈怠者的收入和利润会下降，并与他干活慢下来的程度成比例。可是，若把这10个人放在一个厂商里，让他们作为协作团体一起工作——比如每个人专事某个方面生产——的话，任何不干活成员的成本会均匀地分摊到所有成员身上，因此，如果利用厂商来组织生产，那么，个人承担的怠工成本将小于每个工人也是利润的剩余索取者的情形。而且，在一家厂商内部，计量一个群体中每个人的产量也更为困难，因为他们是一起工作的。所以，仔细拟定出合适的刺激制度来奖励较努力工作生产出较多产量的工人也就更加困难了。这些就是在厂商的组织中起对抗作用的因素。
为使厂商经营成功，必须找到某些办法来抵消这一不利之处。大多数厂商雇人专门监督别人。这些监督者查明工人干不干活，还试图计量工人的产量。厂商中的最高监督者是企业主或雇主。如果企业主或雇主未能有效地监督别人的话，他（或地）的实际财富地位就削弱了。那些选择为厂商工作的雇员隐含地同意接受企业主的监督。
有时接受企业主监督这一点是很明白的。例如，在中国，雇员有时雇人来直接监督自己的工作。
“中国的长江上有一段水流很急，船由一队苦力拉着逆流而上，由一个监工挥舞着皮鞭催促苦力们。在一次旅行中，一位美国女士惊恐地看到这个监工正鞭笞拚命拉纤的纤夫，便央求人们做点什么来制止这种野蛮举动。很快，船长便告诉她无能为力：这些苦力承担着把船拉过这段水路的责任，是他们自己雇用了这个监工，给了他监督权利。”
协同生产除了有技术上的优势，以及可免去某些交易费用之外，其他因素也增强了厂商这种经济组织的生命力。首先，厂商可以从创出有别于他人的商标名声中得益。商标声誉可以附着在该厂商的所有产品上。存在着可供利用的商标声誉，厂商就可以以较低成本引进新的产品。此外，如果修理保证、销售调整和其他有关活动是由单个组织提供的话，这些活动的成本就较少。其次，厂商可避开政府所施加的某些限制，如税收和控制。例如，一家厂商可以以任一内部价格把资源从一个部门转到另一个部门，这样就避免了在交易受到价格控制情况下会存在的资源使用缺乏效率的现象。最后，厂商的存在能使各生产部门之间保持较好的联系。给参与生产过程的各方制定稳定的规则是有益的。实际上，按照有些人的假定，内部承包制度的衰落在很大程度上归因于它将有的组织形式以及其后对参与者个人的影响。在内部承包制度下，独立的承包者都是在一个工厂里生产，厂商管理部门提供地皮、机器、原材料和流动资本，还安排最终产品的销售。可是，实际的生产并不是由雇员从事的，而是由以计件报酬为基础的承包契约体系进行的。温切斯特连发枪支制造公司就是一家在其大部分生产年份里运用这一制度的厂商。显然，当温切斯特公司发觉个人承包者有买方垄断势力，并且赚得收入的差距产生了某种社会问题和其他困难后，就放弃了这种组织形式。对不同组织形式的实际选择除了在很大程度上取决于管束行为的成本不同之外，还取决于集体生产在签订合同和进行交换方面的优势带来的成本的减少。厂商还容许风险承担同厂商的管理结合在一起，因为当管理者也承担风险时，为了刺激管理者而将风险承担者财富极大化的费用就越低。
限制厂商规模和产量的因素
有3个因素限制了厂商规模和产出率：
1．生产能力
2．交易费用
3．外部供应效应
生产能力
物质上或经济上的因素都会限制厂商产出。例如，在现有技术条件下，要厂商在1分钟内建造1座包括4个卧室的房屋或在1年内建500万座房屋在物质上是不许可的；同样，制造每分钟就能从原矿石中提炼出1000吨纯金的机器在物质上也是办不到的．生产能力直接与规模经济有关。一般而言，生产能力受经济因素制约，而不受社会物质特征制约。
管理控制方面的规模经济是确立生产能力的极限的基础。由于生产规模较大，官僚等级层次较多，即使厂商各机构间的目标不是彼此冲突的，信息的再生产以及（或者）信息的扭曲也会造成损失。中心协调者在决策时所需的各种信息容量也有限。结果增加了不确定性，反过来又给中心协调者和下面各等级层次带来进一步的协调问题。
交易费用
人们倾向于认为厂商是一种组织，它被聚合起来享有与联合生产有关的技术经济。但正如我们前面已看到的，内部组织替代市场交换使交易费用可以内部化，以后可以减少合同的签订和对合同执行的监督。正如威廉森指出的，厂商最突出的优势在于，那些适用于厂商内部而还是厂商之间的控制工具有着广泛的可变性和更大的灵敏性。厂商能够比一方购买者更精确地评价绩效，厂商的奖励和惩罚工具也比外部市场更加精致。厂商还拥有一个比外部市场更有效的解决冲突的机构。但有时边际协调费用的增加超过了从评价绩效和解决纠纷获得的收益的增加，这便构成了限制厂商规模的因素。
外部供应效应
同样一种力量，它支持产业中一个厂商扩张，但又可造成外部规模不经济。在最简单的情形下，每个厂商的扩大是与产业增长成比例的，对产业总产出扩大的限制也就转变为每个厂商都提高供应价格。一个产业出现的困难可能来自：使用较劣质投入品生产较优质产品、运输和原料的费用增加、以通行的工资可雇用的劳动力的供给已耗尽，或其他因素。尽管一家厂商规模不可能大到足以影响生产要素价格，但所有厂商一起行动就会产生外部不经济。这些外部不经济直接转化为增加单个厂商使用的生产要素的价格，从而限制了任何厂商的规模。
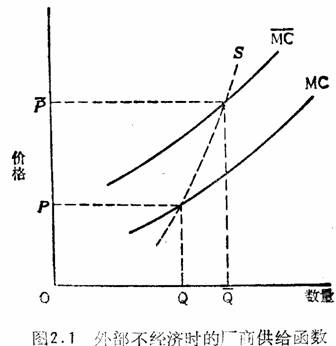
在图2．1中，我们示意一个受制于外部不经济的厂商可能供应的数量。在既定的一组可选择价格下，该厂商的供给曲线由MC所示。投入品价格提高后，厂商边际成本由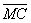
所示。若所有厂商一起扩大，则投入品价格会提高，所以边际成本移到
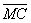。厂商根据价格P愿意提供的数量是Q，对应于另一价格
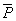愿意提供的数量是
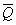。S便代表厂商受外部供应效应限制时的供给曲线。
利润最大化
当我们讨论厂商存在的原因时，我们便隐含地对厂商动机或目标作了假定。据说油水终止于最后的监督者——所有者——企业主或雇主手中。在支付了所有费用之后，他对于剩余下来的资金拥有索取权。这种剩余被称为利润。监督他人的企业主不大会含糊他或她的职责，如果这种监督是与净值直接联系在一起的话。这便是利润最大化的假定，或更确切地说是净值最大化（它的现值在附录中讨论）的基础。消费者理论中效用或满意最大化提供了这一分析的基础。在厂商生产理论中，利润或财富最大化通常是基本的假定。
问题在于，净值最大化假定是否现实？是否可以准确地预见厂商行为？如果我们想要解释企业行为，我们实际上不必假定企业主有意识地努力使利润最大。我们假定他们的行为是与利润最大化一致的－－他们的所作所为好像利润最大化就是目标。有几个类似的情况可以帮助我们理解这一点。若一个物理学家要预言台球球员在何处用球杆击球可把特定的台球打入桌边的一个袋中的话，这个预言台球球员行为的物理学家便假定该球员懂得物理学原理，即使这可能是一个不现实的假定。但我们记得，在第1章对方法论的讨论中我们说过，不必要求假定可以直接检验。其实一般说来，人们是用模型的可反驳的预言来间接检验假设的；若现实世界一致否定了某个模型的预言，则该模型的假定便是正确的。另一个类似的情况是由弗里茨·马克卢普（Fritz
Maohlup）提供的，所用的假想的例子是建立一个汽车驾驶员模型。该驾驶员在双车道公路上开车。他必须注意汽车的速度、位置和加速度；他不但要考虑旁边车道上他要超越的汽车这些相同的变量，而且，他还必须考虑天气和道路条件。只有考虑了所有这些因素之后，才能做出最优决策。显然，驾驶员问题的任何一种严格解法至少要求有一点高等数学知识，但实际所做的并非如此。问题是由经验直觉解决的。赚取利润要解决的问题也是如此。利润最大化模型可以假定存在完备的知识，并且不存在不确定性。可是对厂商经理来说，这种完备的知识和没有不确定性显然是不需要存在的，就好像在双车道上开车的驾驶员不必具备高等教学知识那样。正如驾驶员是本能地作出决策一样，企业中也可按其本能的指引寻求利润最大。
利润的性质
我们把利润定义为收益与成本之差。在短期内为使利润最大，厂商将使短期边际成本等于边际收益。在长期竞争中，平均单位成本会等于边际成本。正如我们以前所提到的，利润可视为付给承担风险的企业家的剩余。
利润函数
利润为消费者控制生产者提供了一种主要工具。利润的暂时变化常常出自消费者从一种产品到另一种产品的较大的需求转移。注们假定偏好的变化引起对某种商品需求的增加。在现有生产得以扩大以前，消费者出价购买现有产品和存货，由此会引起价格提高，并且在绝大多数情况下带来更高利润。这些利润反边来又提供了信号，使各个制造商扩大生产，也使新厂商进入并开始生产在当前有更高价格的物品。结果，资源就流到了销路好、利润高的行业。这种流动造成生产量更大，价格更低，资源配置得到了攻善。
传统利润理论
当物品和服务卖出后，劳动、土地和资本所有者就得到了工资、地租和利息。现在的问题是，为什么支付给劳动、土地和资本所有者的数额的加总并不等于从出售中获得的收益？换句话说，为什么应该有东西剩余下来？为什么应该有利润（它是扣除所有成本之后的剩余）？为了回答这个问题，我们必须提出一个为何存在利润的理论。不幸的是，我们还不能提供一个唯一的为人接受（或可以为人接受）的利润理论。作为替代办法，我们提出3种为何存在利润的可行的理由。这些理论必须与承担风险、不均衡和垄断势力有关。它们并不是相互排斥的。
承担风险
有一种利润理论认为，利润是承担风险的报酬。任何一个获得一个新企业的机会的人都易遭受失败风险，或遭受这次投机中所赚要小于其他投机所赚的风险。从事契约劳动的个人则在很大程度上避免了这种风险。他们可以签订长期合同，以保证特定的工资率。土地（或自然资源）所有者也同样这么做。但企业所有者无法与某种“更高势力”订合同以保证收益超过成本。如业业经营失败，承受财富或净值减少的就是所有者，这是显而易见的。而且，企业确实会失败。有些研究表明，每3个新开办的小企业中，就有2个最终归于失败。显然，为使企业家承担风险，人们必定期望付给他的报酬超出正常的补偿。这就是说，获得经济利润的可能必须包含在未来中，以使企业家接受风险。
必须酬劳或补偿承担风险者的理由在于绝大多数人看来并不喜欢风险。考虑这样一个例子：有人向你提一个经营建议，你必须投资1000美元。损失1000美元的机会是50％。另一方面，多赚1000美元（总收益是2000美元）的机会也是50％。该建议的期望值是零：－1000＋（0）（0．5）＋（2000）（0．50）。你愿意做这笔生意吗？也许不会。为了使你承担丧失你所有的钱的风险，必须付给你更多的报酬。
有些企业经营失败了，有些没有失败。若我们权衡一下亏损和利润，我们便会发现平均赚得的经济利润为正。根据利润风险理论，其原因在于对不喜欢风险而又承担了风险的企业家给予补偿。如果企业家是寻求风险型的，他们可能会以零或有时是负的期望值来承担风险。
不均衡
另一个利润理论涉及背离了均衡的市场。市场不均衡是指挣得的收益率高于或低于正常收益率的情形。我们还记得完全竞争情形下，长期均衡时所得经济利润为零。我们一直处于向长期均衡的移动过程之中，因此，在短期中一般是不均衡的。设有一例，此时对某一特定产品的需求突然增加。第一批觉察到这种需束增加的企业家能够进入市场，他们的生产和销售计划可以在别人赶上来以前得到调整。由于他们认识到这种瞬间的不均衡，因而得到的报酬高于正常收益，即他们会得到经济利润。
同样的分析对于供给方也可成立。某些认识到新的可利用生产方法的企业家可以赚得较高利润，他们可能力图占据知识上的优势。他们把新的生产技术付诸实施，并确实暂时赚得了经济利润。
注意这里经济利润是暂时性的。根据这个利润来自不均衡的理论，长期中如果没有预见到的事件改变供求的话，则所有经济利润都会因竞争而消失，所赚得的只是正常的（会计）收益率。
暂时利润也可以是负的。对某种产品的需求突然下降会降低该行业的收益率，直到削减失产以及（或者）厂商离开该行业为止。收益达不到补偿企业家所必须的数量．同样，生产成本的暂时增加会暂时降低供万的利润，这又导致减少产量和退出该行业。
不完全竞争
第三个利润理论与垄断势力有关。我们已经指出追求利润最大的垄断者会减少产量，提高价格。该垄断者因而可能得到垄断利润，只要垄断者可以阻止别人进入该产业，垄断利润甚至在长期中也可普遍存在。因此，这不是不均衡利润理论。
批评垄断利润理论的意见认为，这种利润只是在短期中才存在（尽管这也许是很多年），永久性阻止进入一个行业毕竟是很困难的，即便借助立法手段也是如此。垄断者必须凭借其在市场上的不寻常地位，耗费资源以保护其垄断地位，为此所耗费的资源最终可能蚕食掉垄断利润。因此，根据批评垄断利润理论的意见，这种利润近似于不均衡经济理论因为他们只是暂的。
这些理论并不互相抵触
我们已经给出了3种经济利润理论，它们并不互相抵触。每一种理论都有助于解释经济利润存在的原因。
其他可供选择的厂商理论
20多年来，大家对厂商理论——或管理者行为理论——一直争论得非常激烈．因为人们不满足于用传统的利润最大化公理预言厂商行为。有些人认为，经理或管理者的开支超出了厂商财富达于极大所必需的开支。他们声称，从管理者行为看，厂商的目标好像是使资产最大或使雇用人数最大。不满于传统利润最大化理论的一个结果，便是引入了许多新的、与原有理论竞争的厂商行为模型。这些解释看来依赖于某个经理特定动机方面的差别。可以分为3大类——单变量效用函数最大化、多变量效用函数最大化以及非最大化模型。
第一类由一个单时期模型，如利润率或销售率最大化模型，和一个跨时期模型组成。后者用多时期资本值或增长最大化准则代替了单时期利润或销售额最大化目标。第二类所包含的模型，在厂商经理的效用函数中，除了认定为数众多的事物以外，也认定这些事物之间此消彼长互为替代的关系。这些事物可分为：经理可得到的货币收益和非货币收益，以及管理人员从分配给厂商内部和外部的个人报酬中可得到的收益。
由于在股份公司中所有权是分散的，所以，最常用的管理者行为模型集中注意管理者在货币财富（利润）和额外的经理效用来源如闲暇、安全、社会责任和权力（无论怎样定义）之间的权衡取舍。存在如此之多的相互竞争的管理者行为理论的原因，部分在于难以检验这么多的解释，部分在于现有组织的社会和制度设置方面存在着差别。这些相互竞争的模型之间可以预料到的差别，显然有大部分可以解释为是各种所有权和与此相联系的引导个人行为的惩罚与奖励的结果。这就是说，人们可以设计一种刺激制度，它对个人行为作出的预言将与这些模型作出的预言相同。表2．1表明了主要厂商理论的分类。我们现在要更仔细地考察其中的一些理论。
职员人数最大化
只要存在企业的所有权和控制权的分离，就会出现管理者不按最有利于所有者的方式活动的可能性。既然监督本身是代价很高的活动，因此企业所有者对于管理者为自己的利益而牺牲所有者利益的一些活动不会有力图加以彻底消除的动机。以所有权和控制权分离为前提，经理能够寻求某些产生效用的资源组合，这些组合的目标在于满足他们自己的效用，而不是实现所有者利润或财富的最大化。例如，管理者可能要牺牲一部分所有者的利润来增加职员规模，尤其是在即使管理者不百分之百地按所有者利益行事，要“抓住”管理者把柄也很困难的时候。我们可以用无差异曲线显示这种权衡。在图2．2中我们画出3条线。
表2．1主要的厂商最大化理论分类表
_____________________________________________
理论分类
理论
_____________________________________________
单变量准则模型
_____________________________________________
单时期 1
利润最大化
2
销售额最大化或资产最大比（受利润条件约束）
3
组织松弛最大化
多时期 1
财富最大化
2
销售增长率或产出增长率
3
销售额现值最大化
4
目标收益率
____________________________________________
多变量效用模型
在以下因素间 1
利润和闲暇
权衡
2 利润和厂商内部和睦的气氛
3
经理利润和所有者利润
4
利润和控制
5
利润和安全性
6
利润和社会责任
7
利润和产品的尽善尽美
8
利润和既达到厂商内部气氛和睦又达到外部气
氛舒畅
9
利润和经理的相机抉择
10
利润、产出和薪金
11 利润和其他非货币报酬
12
利润和某种资产组合
13
利润和职业美德
14
利润、地位、权力和威望
15
利润和职员规模
________________________________________
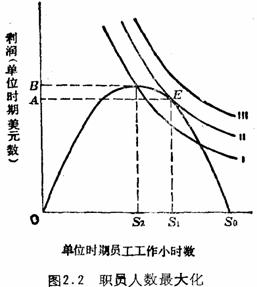
单位时期职员工作小时数由横轴所示，利润表示为纵轴上单位时间美元
数，从0到S2，职员人数增加时，利润也增加，在S2点之后利润下降。因此，使
利润最大的职员规模点在S2点；然而，如果假定经理从增加职员人数中可获得
效用，那末，经理雇用的职员人数会达到他们无差异曲线族中最高的那条无差
异曲Ⅱ上的一点，即图中的E点，雇用的职员人数为S1，它大于S2。对应的
利润A将小于最大利润B。
图2．2横轴度量单位时间内员工工作小时，纵轴度量单位时间利润。假定管理者无差异曲线凸向原点，利润曲线表示利润和职员规模的关系。随着职员的增添，利润递增到最大值B时，相应的职员规模为S2，随着职员人数的继续增加，利润相应递减，直到职员规模在S0处降到零。管理者效用达于最大的职员规模S1，即无差异曲线Ⅱ与“预算约束线”（或利润与职员规模之间的此消彼长互为替代曲线）相切之点E。如果不存在所有权和控制权的分离，或者假如由所有者本人进行监督无需花费代价，那末，除非所有者自己偏好雇用较多的职员，否则，职员规模将全定在S2。利润便是最大值B。换言之，管理者本来可以代表所有者定出最优职员规模。
这便是一个管理者行为的效用最大化理论。它要求存在这—情况，即所有者或股东获得信息的代价颇高。它也要求厂商具有某种程度的市场势力。如果厂商处于完全竞争市场，只有力求利润最大才能生存下来，除非所有者决定把一部分收入花在职员身上，或所有厂商都表现出同一行为。
销售额最大化
另一个厂商模型是以销售额最大化理论为基础的。如果经理认为，他们自己的报酬以及（或者）其职业威望更主要是取决于销售量而不是利润的话，他们可能追求销售额最大是取决于销售量而不是利润的话，他们可能能追求销售额最大
化。我们在此必须加进一个约束条件，即股东的确要求投资要有一个最低收益率。注意我们现在谈到的是利润率－－或者每年利润／投资－－而还是绝对利润。
销售最大化模型由图2.3所示。
假定在Q1之前盈利（用投资收益率来表示）是总销售额的递增函数，在Q1
后，盈利率下降；还假定存在一个经理必须满足的最低年收益率10％，经理的
无差异曲线是Ⅰ、Ⅱ、Ⅲ。它们是垂直的，表示经理并来从盈利状况好本身得
到效用。经理可达到的最高无差异曲线不是Ⅲ，销售率也不在Q3，因为每年销
售额产生的盈利低于10％，因此经理力求达到的销售额为Q3，此时正好在无差异曲线Ⅱ上，注意该销售额大于利润最大时的销售额Q1。
图2．3表示销售额最大化模型。纵轴代表用投资收益率表示的利润，横轴代表单位时期的销售额。利润率和销售额之间的关系如曲线所示；利润率在销售额为Q1处达到最大。但是，假定最大收益点（价格乘数量）在销售额为Q3处。尽管管理人员希望使销售收入最大，产量也无法达到Q3。因为已经对它施加了约束条件——最低收益率。我们将最低收益率任意划定为每年为10％，因此，管理者将把销售额定在Q2，而不是定在利润最大时的Q2处。
你会注意到我们在图2．3中画了垂直的Ⅰ、Ⅱ和Ⅲ无差异曲线。因为我们假定无论盈利性多大，管理部门都得不到效用。因此，更高的效用曲线只是向右移动的垂直线。管理者怎样才能增加单位时期的销售额从而增加收益呢？假定他们的生产正好处于需求曲线有弹性的部分，经理便可降低产品价格来增加总收益。而且，经理可以把需求曲线向右上方移动，做更多广告来增加销售额。一些对销售额最大化假定所做的经验研究采用了威廉·J·鲍莫尔（William
J．Baumol）提出的检验方法。他认为：“经理的薪金与厂商生产规模的相关关系似乎比与利润率的相关关系密切得多。”鲍莫尔在1967年修订版书中，把销售额最大化假定修改为销售额增长率最大化。这样，他就用多时期销售额最大化假说取代了单时期销售额最大化假说．麦圭尔（McGuire）、邱（Chiu）和埃尔宾（Elbing）检验了这一假说，发现经理人员收入和销售额（经营规模）的相关性比经理收入和利润的相关性更高。他们的结论是：鲍莫尔的假说得到了这些结果的支持。马布里（Mabry）和赛德（Siders）进一步检验了鲍莫尔的假说，得出的结果弱得多。他们的研究成果提供的证据既未支持、也未拒绝销售最大化假说。马歇尔·霍尔（Marshall
Hall）作了进一步的检验，他并没有发现支持销售额最大化的证据。霍尔模型的一个含义是。现期销售额的增加部分地可由过去利润来解释，而这一利润是大于隐含的利润约束的。贝克（Ba－ker）用新的数据来检验销售与利润之间的相关性。他的结论是，无论是利润还是销售额，对于最高管理者的报酬都没有独立的影响。
增长最大化
一个类似的厂商模型是增长最大化模型，即经理致力于使销售收入增长率最大化。这大约也可以解释为何经理们如此乐意与其他厂商合并。如果他们发觉自己的薪水与厂商增长率有关，以及与把更大组织置于他的影响下有关，便会扩大厂商的活动。但是，他们仍然会受一定盈利性要求制约。在理论上，这种盈利性要求存在的理由是：若盈利性太差，一些股东也许会接管该厂商（以及解雇一部分或全部现任经理）。
加尔布雷思的观点
约翰·肯尼斯·加尔布雷思在其《新工业国》和《经济学和公共目标》中提出的观点，把管理者效用最大化、销售额最大化和增长率综合起来了。他指出，经理追求的是威望和技术熟练技巧。他还指出，经理可以实现其计划的原因，在于他们能够影响消费者行为，办法主要是做广告。因为股份公司是由那些希望自己过舒适日子的经理们经营的。所以加尔布雷恩强调大股份公司会力图避免风险，制订广泛的计划来增加稳定性。这种所谓的经济计划部门是由股份公司的技术专家经营的。后者是技术熟练的个人。在加尔布雷思看来，他们作出了所有重要的经营计划决策。
多变量模型
有些作者不是用别的单一变量去代替目标函数中的利润，而是扩大函数中的变量个数。例如阿门·阿尔钦和鲁本·凯塞尔（Reuben Kessel）提出了一个经理行为的效用最大化假定。他们把非货币动机加入了目标（效用）函数。这一含意在拥有较高程度垄断（封闭的市场）势力的厂商那里，得到了一些经验上的证实。例如，人们发现这些厂商不太强调雇员之间的货币生产率差别，而更强调个人的人身方面的特征（相貌、个性、宗教、种族等等）。有时，这些特征被用作判断雇员是否合乎意愿的标志。此外，罗斯·埃克特（Ross
Eckert）还单独对管制专员（regulatory
commissioners）的行为进行了检验。所提供的证据证实，当管制专员面临某种制度约束时，他们确实以可预见的方式活动。这种制度约束使得对管制专员某种活动的酬劳多于或少于追求利润的组织的经理面临的刺激。例如，在专员从进一步管制中得到的好处不多时，就显露出对扩大管制活动没有什么兴趣。奥立弗·威廉森提出了一个有所不同的分析方法。他也扩大了经理目标函数中目标的个数。但在扩大个数时，威廉森仔细地罗列了效用函数所包含的内容。根据他提出的假说，经理可以用3种确定方式之一增加其效用：
1．靠为所有者获取更多财富来增加薪金；
2．以牺牲所有者更大利益为代价，靠扩大销售和资产来增加其薪金；
3．在所有者财富与非货币的效用源泉（更大的办公室、更厚的地毯、送礼更慷慨、更宽松的人事政策等等）之间的权衡取舍。
威廉森与鲍莫尔不同。他采用的约束条件既包括最低的或可接受的利润水平，也包括资本市场约束。威廉森提出的证据表明，在运用于某种情况，如对利润税或一次性总付税所作的反应中，他的效用最大化解释比古典理论更好地预言了经理行为。在其他场合（如需求的变化和对销售税的反应），他的模型正如古典利润最大化理论一样可靠。
选择经理行为理论并不容易，经验上的发现也没有改变这一点。例如，威廉森声称阿尔钦－凯塞尔假说是他的模型的一个特例：
如果资本市场（既包括股东也包括厂商的债权者）施加给管理人员实绩的约束条件较松的话，管理人员就更自由地随意行使厂商拥有的垄断势力。因此，尽管我们完全赞同阿尔钦－凯塞尔对非货币动机的讨论和他们用一般偏好函数代替利润函数，但我们还是认为，受管制行业只不过是一般情形的特例。这种一般情形是，由于存在着混合合并巨头或进入壁垒的缘故，产品市场上的竞争很弱。
但是，人们也可以说阿尔钦－凯塞尔理论是更一般的假定。威廉森注意的是范围很狭窄的薪金与“支出偏好”之间的权衡抉择，而阿尔钦和凯塞尔则列出了一个一般偏好函数，分析在各种约束情况下的行为，包括产品市场和资本市场缺乏竞争的情形。
重要之点不在于垄断性厂商和竞争性厂商之间存在着偏好上的差别，而在于用货币收入换取非货币收入方面存在着差别。如果有关价格或交换比例方面的差别给定的话，所购买的品种存在差别也就不足为奇了。
回顾一下表2．1便可知，不同多变量函数的变形相当多。在60年代和70年代，仿佛存在一场竞争，各路研究者都在寻找新的变量，将之放入效用函数中去。融合了这些不同的变量说明之后，利润仍然是一个重要的解释变量，尽管人们发现厂商规模也很重要。此外，像麦凯瑟（Mceachern）这样的研究者已经指出并证明，在所有者并不积极参与管理的公司里，所有权结构本身便是决定最高管理者报酬的因素。麦凯琴发现，这种报酬与盈利率的正相关性比它与销售收入的正相关性更强。
令人满意的行为
根据厂商行为的令人满意的行为理论，厂商给自己定了最低绩效标准，其目标是令人满意的利润率；可以假定，一旦达到这一利润率，厂商便会懈怠下来。令人满意的厂商行为理论的一个含义是，倘若可以赚得一个令人满意的收益率的话，那么，厂商内部并不始终存在着使既定产量水平下的成本最小的努力。换言之，存在着内部松懈。
对非利润最大化假定的批评
批评意见除了针对假定在经济理论中的作用问题外，还直接针对上述各种模型。一种批评意见认为，经理市场确实是存在的。每个厂商的管理班子都面临这种可能性：另外一些管理班子可以说服股东相信，如果让他们来控制厂商，他们会增加厂商的盈利性。如果存在股份公司经理人员的市场，那末那种急剧偏离利润最大化假定的管理者行为就不会被允许无限期持续下去。但是，很明显，控制股份公司管理人员的阻力越大，厂商便越是可能在一个非利润最大化空间里经营。
而且，批评非利润最大化厂商模型的意见还指出，不仅要考虑现有的股东，还要考虑潜在股东。应记住，资产价格是其预期未来净收入的贴现流量。如果涉及的资产是厂商的普通股，则它在市场上的价值或价格就是预期未来净利润的现值。因此，若当前管理人员的决策不能使长期利润最大，则该厂商股票的当前市场价格就会低于其他情况下的价格。有些人可能会注意到这一点，这样该股份公司就会成为提议接管者的猎物。一群投资者可能试图以目前的低价买下该公司较大份额的股票。用这个办法接管该公司后，他们就解雇目前的经理，委任新经理，从而增加预期未来收益率。这样股市又会上升。接管者得到的净值——资本收益——便增加了，因为他们现在拥有的公司股票卖价超过了当时的买价。因此，当存在接管股份公司的市场时，就有某些限制来约束非利润最大化行为。
经理偏离利润最大化到什么程度，主要取决于新经理接管厂商的交易费用。斯迈里（Smiley）估计，厂商股票的市场价值要降到低于其潜在价值13％左右，接管才成为可能。此外他还估计，由于1934年证券交易法的1968年修正案（威廉姆斯（Williams）修正案）严厉限制用现金投标出价和接管，因此就把投标出价的成本增加了27％。
调和折衷
非利润最大化假说的一个最引人注目的方面，是大厂商的经理可以经常公开地牺牲股东的利益来为自己谋好处。幸运的是，詹森（Jensen）教授和梅克林（Meckling）教授已经提出了一个严密的理论分析。他们指出，管理人员额外消费收入现象的出现及其程度与厂商价值最大化是不矛盾的。这两位作者认为，“代理费用”（agency
oosts）阻止了纯粹追求利润最大的雇佣经理人员的存在。尽管如此，厂商的价值在扣除这些成本之后仍可最大化，这些成本是真实成本，相当于工资、原材料等成本。詹森－梅克林假说代表了一种很有前途的开端，即把各种主要的、又是经常相冲突的非利润最大化分析调和折衷起来。
附录A：定价和产量决策
即期行业定价
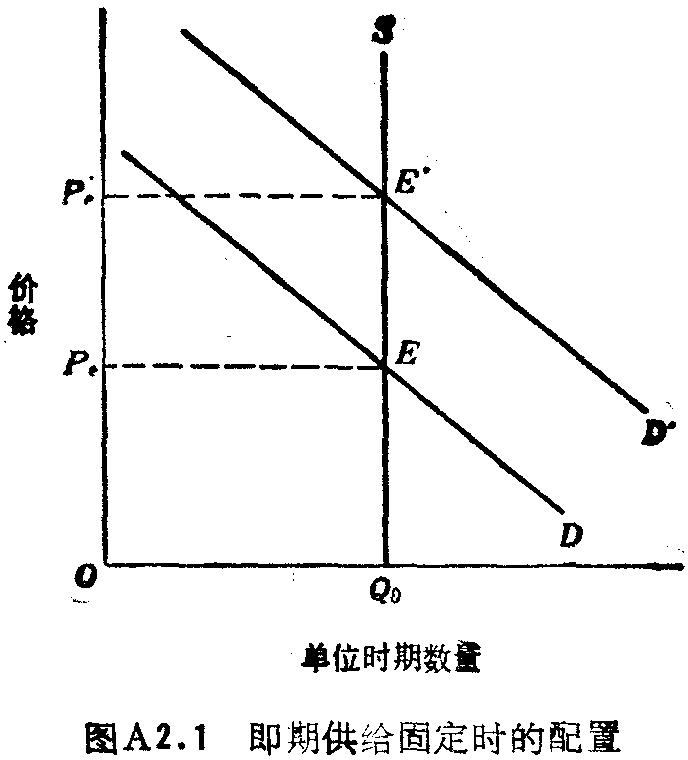
首先让我们来考虑即期（交易日，或极短期）的价格，此时时间不允许产品的供方作出调整。供给曲线是完全无弹性的，假定该行业是任何一组生产同质产品的厂商。见图A2．1。
市场需求曲线由所有个别需求曲线水平加总而来。在即期（交易日）中，供给曲线是垂直的，均衡点Qo唯一地由供给决定，市场是出清的或均衡的，价格由市场需求曲线DD与SS的交点所决定（即价格Pe）。若需求增加到D’D’，市场出清价格就会增加到P’e，即均衡数量将仍是Qo。
完全竞争厂商面对的需求曲线
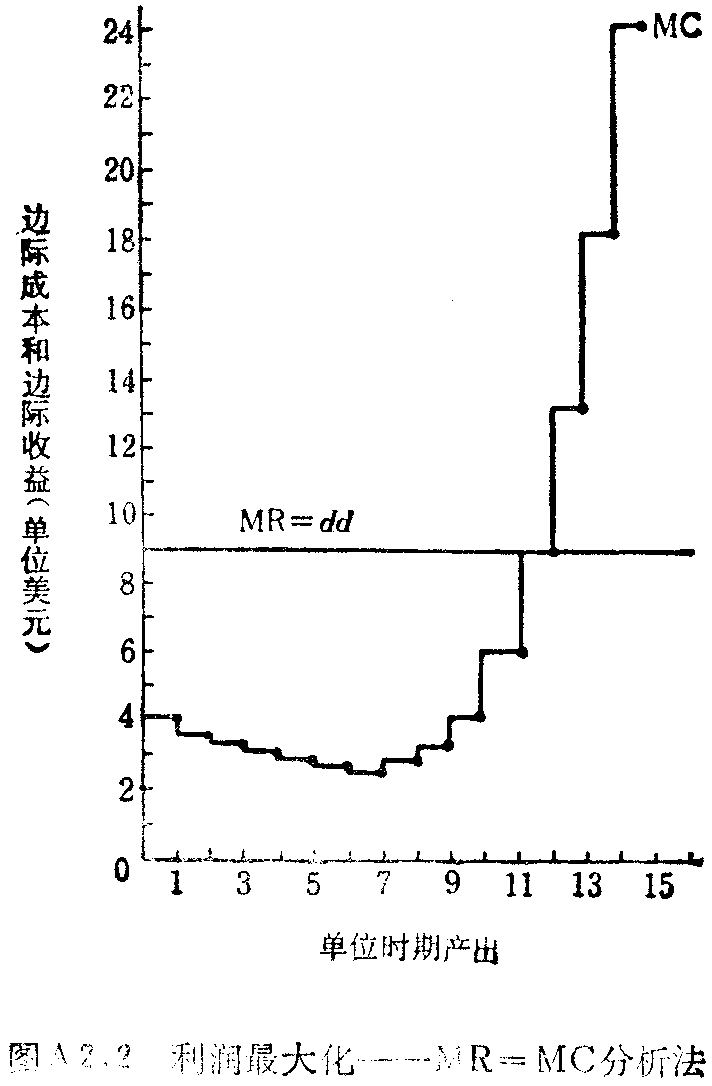
一个完全竞争行业中的厂商无法影响所售商品的价格，而必须把价格视为既定。市场出清价格或均衡价格由市场需求和市场供给的交点决定。既然价格是既定的，因而单个厂商面对的需求曲线看上去就会像图A2．2中的dd。这里9美元便是“通行价格”（由市场需求曲线和市场供给曲线的交点决定的均衡价格）。其价格弹性η＝∞，即完全弹性。
完全竞争者的边际收益
边际收益是单位销售量的增加所引起的总收益的变化，它与需求的价格弹性有关：
在完全竞争行业中，需求的价格弹性等于－8，因此该等式变成：
因此，对于完全竞争厂商来说，边际收益等于价格。
利润最大化
当边际收益等于边际成本时，利润就最大。对完全竞争厂商来说，边际收益与其需求曲线dd是一样的，它是在每单位9美元处的水平线。
短期损益相抵价格及停止生产价格
任何一条价格线都代表了完全竞争者的边际收益线，使利润最大的产出率总是位于价格线与边际成本曲线相交处的产量上。右图A2．3中，短期损益相抵点是E点，短期损益相抵的价格是P1，该价格正好补偿平均总成本。短期停止生产点为E’，短期停止生产价格为P2，它等于最低平均可变成本。如果它不能至少补偿可变成本的话，厂商便无法继续生产。
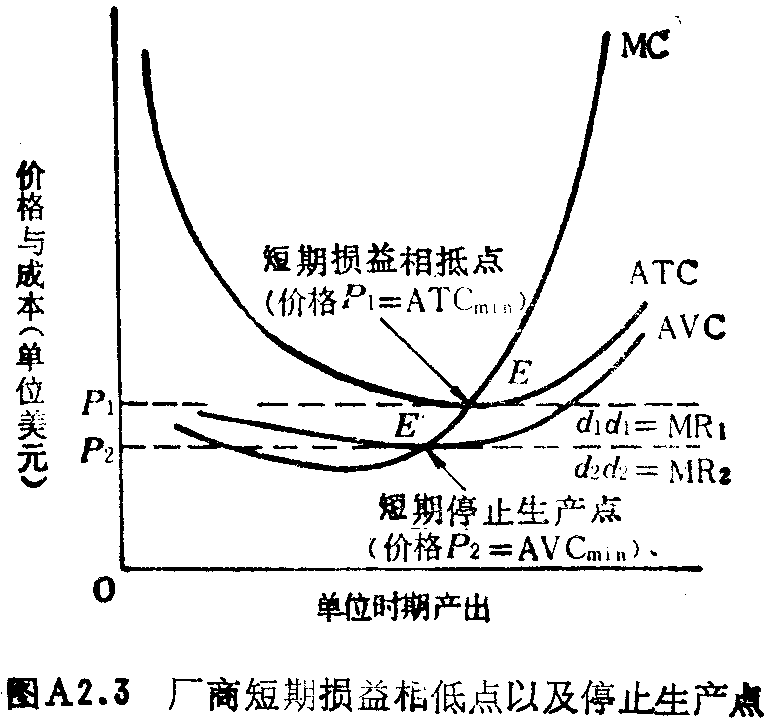
市场均衡和厂商最优规模
图A2．4表示市场均衡和厂商最优规模。在图（a）中，市场需求曲线为DD，市场供给曲线为SS。它们相交于E点，市场出清价格为Pe，市场出清数量为Qe。Pe是图（b）中的完全竞争者面对的需求曲线。厂商边际成本曲线交dd于e点。由完全竞争厂商生产的利润最大的数量是qe。
长期均衡下厂商的厂房设备的调整
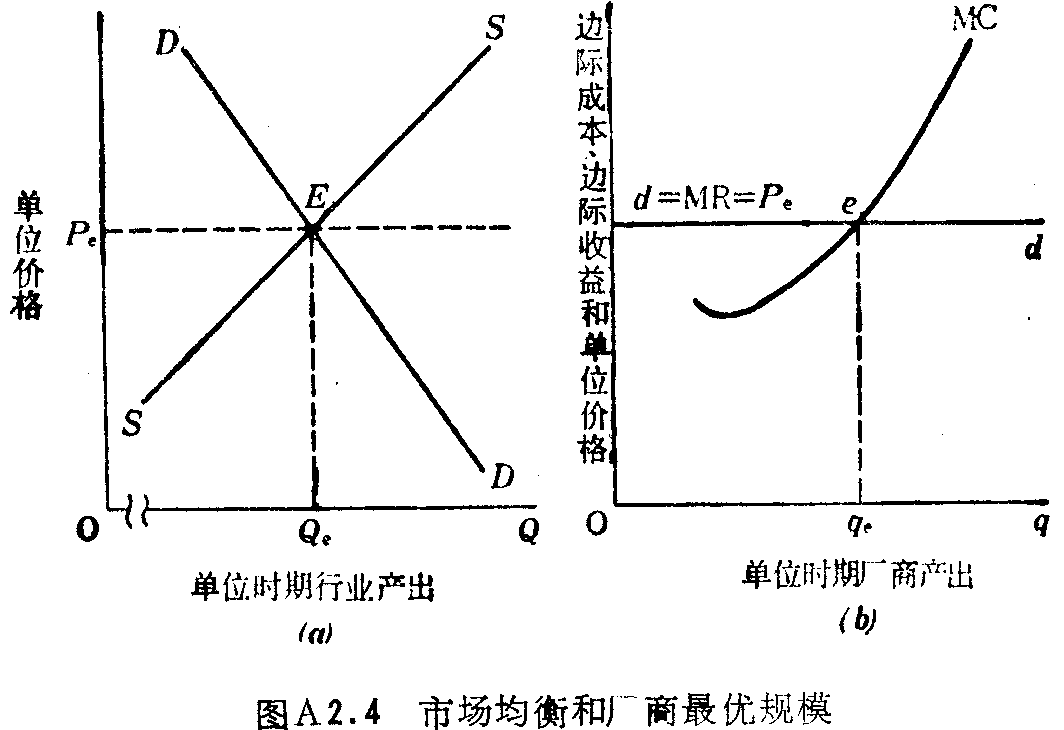
在长期中，厂商可以改变其工厂规模。在图A2．5中，若长期均衡价格为P1，工厂的最优规模不是由SAC1（短期平均成本）和SMC1（短期达标成本）络定的。因为，在该工厂利润最大的产出处q1，厂商不是根据长期平均成本曲线LAC来生产的，该厂商会扩大工厂，直到其成本曲线由SAC2和SMC2
给定为止．使利润最大的产出率为q2，厂商根据LAC生产，单位利润从P1和C1间的纵向距离增加到P1和C2间的纵向距离。
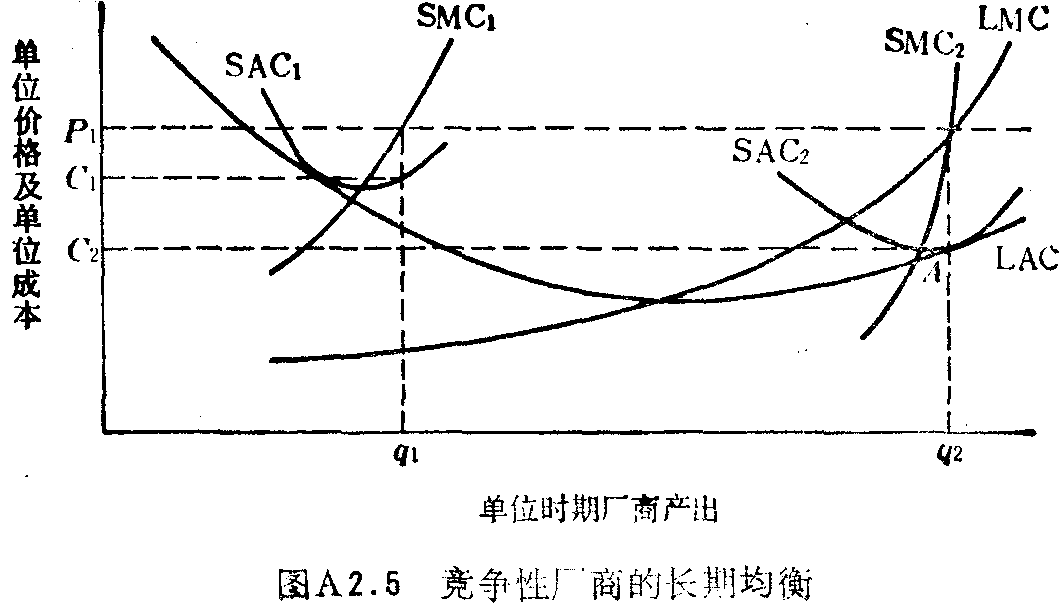
长期竞争性均衡
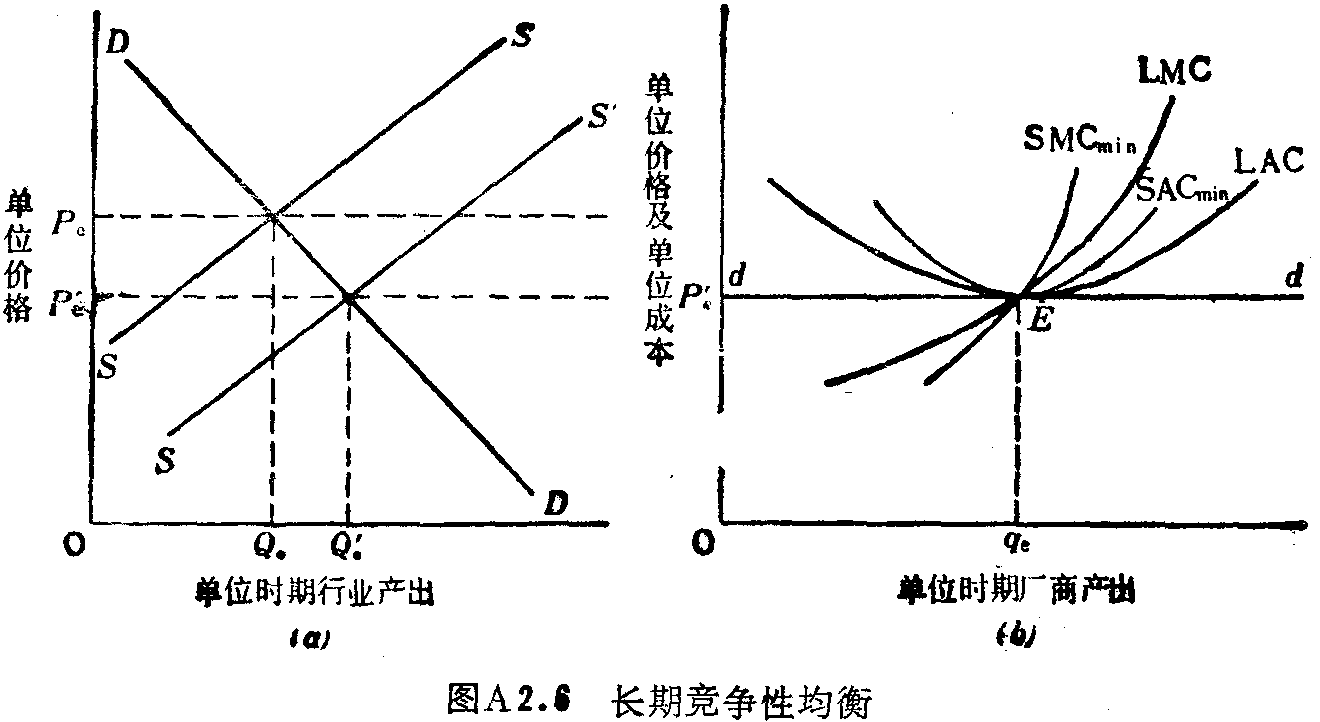
经济利润会促使其他厂商纷纷进入该行业。在图A2．6中，若现有厂商获得了经济利润，进入该行业的现象就会出现。图（a）中的供给曲线就会向右方移动，从SS转向S’S’，行业产量从Qe增加到Q’e；平均出清价格从Pe降到P’ee最终厂商就会发觉自己处于图（b）所示的境地。这时，在利润最大的产量Qe处LAC＝LMC＝P’e＝SMC＝SAC。既得不到经济利润，也无亏损。
长期供给调整
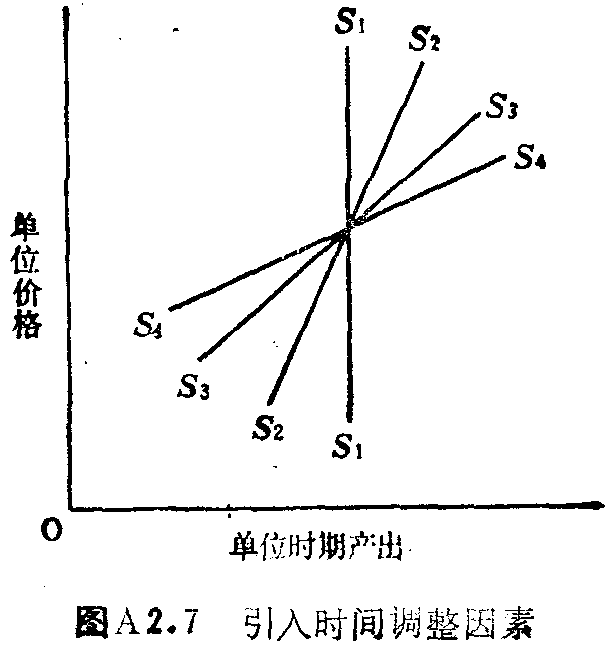
如同需求曲线一样，在其他条件不变时，长期供给曲线会比短期供给曲线更有价格弹性。在图A2．7中，即期（交易日）供给曲线S1S1是垂直的，其价格弹性等于零。允许调整的时间越长，则它犹越有弹性，从S1S1移向S2S2等等。
垄断定价和产出
单个垄断卖者面对的需求曲线也是行业需求曲线，它是向下倾斜的。在该曲线形成时，我们要假定垄断者对所有购买者的售价都是一样的，即不是歧视性垄断。
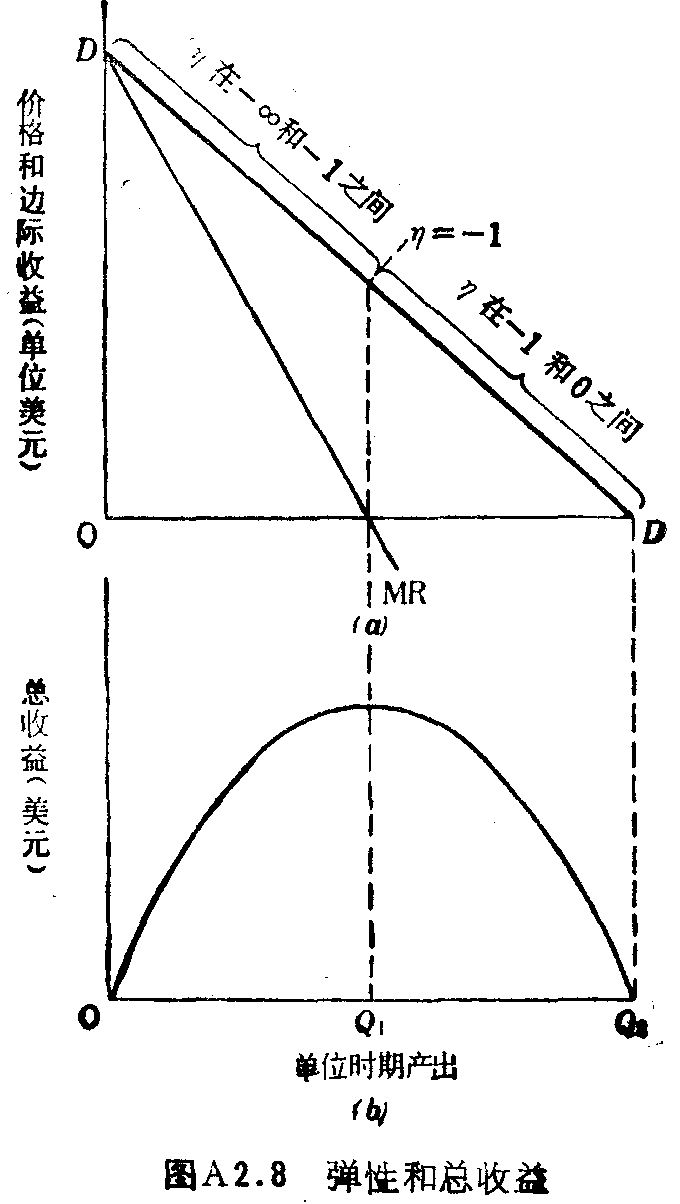
在图A2．8的图（a）中，我们画了一条线性需求曲线，沿着该曲线数量增加时，需求的价格弹性就减少。在需求曲线的中点，需求的价格弹性等于－1，边际收益等于零。在图（b）中，我们可以看到总收益的起点是零，在产出率为Q1时达到最高值，然后下降，到产出率为Q2、价格为零时降到零。在η＝－1的产出率处总收益最大。
因此，从图A2．8中可清楚地看到，垄断厂商决不会在大于Q1的产出率处生产，因为此时边际收益为负。这等于说垄断者决不会在需求曲线DD的无弹性部分中进行生产。
垄断边际收益
垄断厂商决不会愿意在边际收益低于零处生产。因为即使生产成本为零，垄断者也总是可以减少产量，从而增加收益和利润。
利润最大化
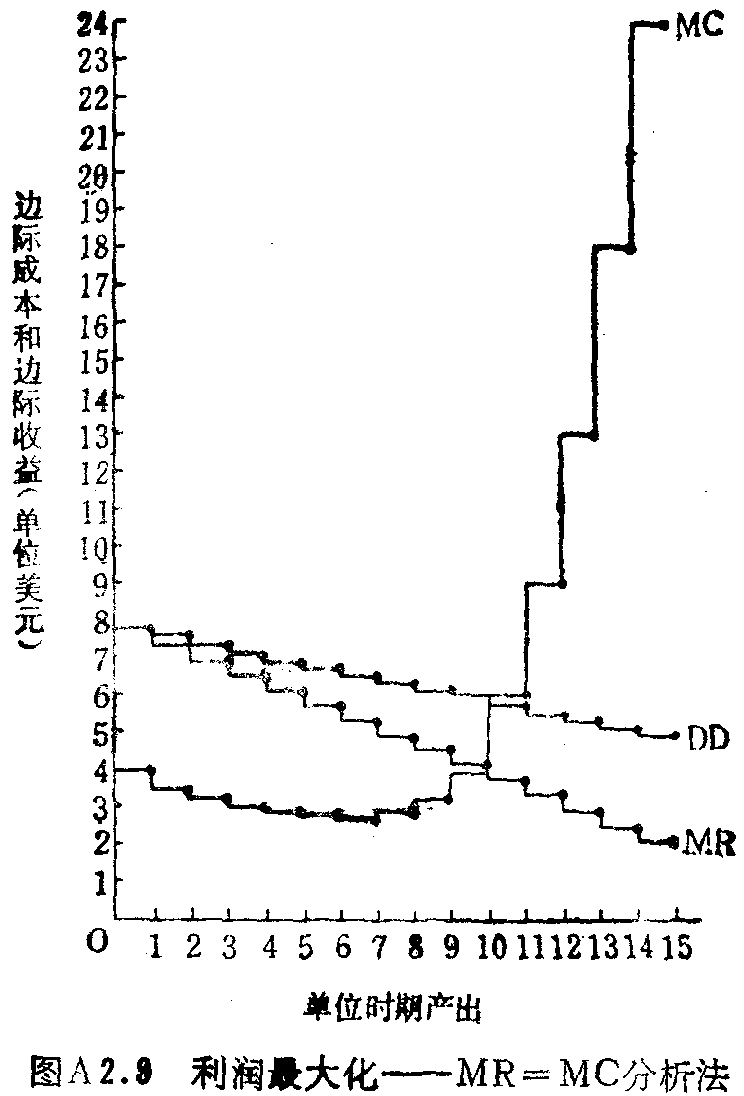
不完全垄断时，利润最大化发生于边际收益等于边际成本处。在图A2．9中，即发生于产出率约为10处。（而且，边际成本曲线必须从下面同边际收益曲线相切。）
记住，完全竞争者总是在平均成本曲线最低点生产。如果垄断者长期平均总成本不变，他也可这样生产，使平均总成本最小。这样，垄断者便会在短期平均总成本曲线的最低点处生产。因此，纯粹的竞争和垄断理论之间唯一必要的、有说服力的区别是：垄断者的价格超过边际成本，而竞争者的价格等于边际成本。
垄断者的供给曲线不存在
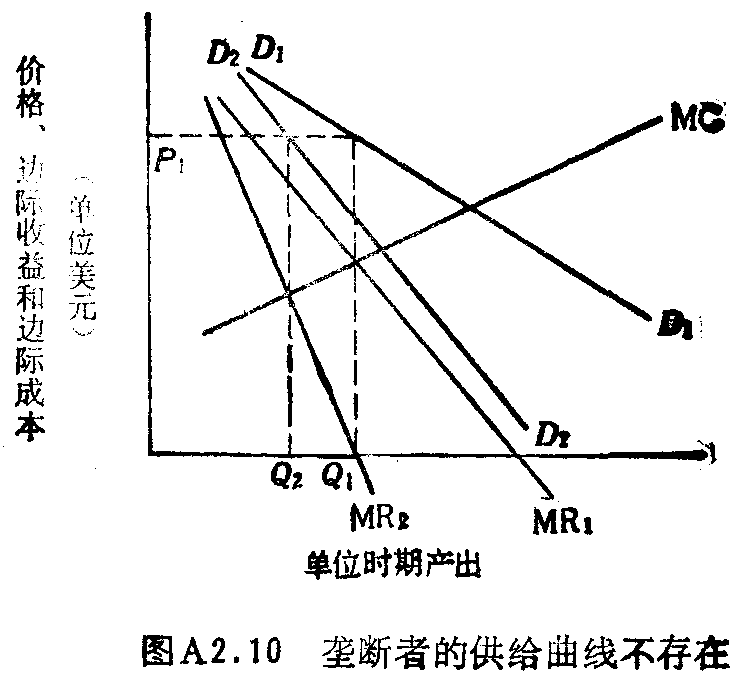
因为供给曲线的定义是与生产者会提供的任一给定产量相应的最低价格的轨迹，所以对垄断者这样的厂商来说，是不存在供给曲线的。在图A2．10中，我们画出两条不一样的需求线D1D1和D2D2，使利润最大的价格恰好相同，但垄断者供给的数量不同。因此，在垄断者供给的数量和价格之间没有一一对应的联系。
附录B：现值准则
在时间变比中利润最大化是指净值最大化，这等同于使所有未来利润的预期流量现值最大。为了了解什么是现值，我们来考察贴现和现值的计算。
从现在起1年后得到的110美元的现值是多少？这取决于市场利息率。如市场利率为5％，我们可用回答这个问题来指出现值：“今天我必须在银行中以某种市场利率存多少钱，从现在起1年后才会给我带来110美元？”或
（1＋0．05）P1＝110美元
（B2·1）
此时我们必须把P1放在一边。
解此方程，我们得到
P＝110美元/1.05＝104.76
（B2．2）
也就是说，当市场利率为5％时，1年到期后104．76美元累积成110美元。这样，现值公式就是
P1＝A/(1＋r)
（B2．3）
这里
P1＝从现在起1年后被付给或得到的货币的未来值
A＝从现在起1年后某数额的现值
r＝市场利息率
较长期的现值
容易看出，现值公式指明了在未来时期所收到的美元的现值。如果付给帐户每年5％的报酬，每年按复利计算，必须在今天的户头上存入多少，才能从现在起2年后得到110美元？
1年后，先把P1撇开不说，就已增加到P1（1．05美元）；第2年后该数额就会增加到P2（1．05美元）（1．05美元）或P2（1．05美元）2。为解出每2年结束时将增加到110美元的P2，设
P2（1.05美元）2＝110美元
（B2.4）
解出P2
P2＝110美元/（1.05）2＝99.77美元 （B2.5）
因此，从现在起2年后被付给或收到的110美元的现值，扣除每年按复利计算的5％的年利率，等于99．77美元。换言之，若每年复利为5％，把99．77美元存在户头上2年后就累积成110美元。
贴现一般公式便成为
（B2.6）
这里t是指未来被付给或收到货币的年份数。表B2．1给出了不同利率下，从现在起t年后得到1美元的现值。用来推算现值的利率常常称贴现率。
我们在例子中已详细列举了贴现率，它是储蓄时可利用的市场利率（这种特定比率不可能总是合适的）。注意我们有2个重要结论：
1．在既定贴现率下，被付给或收到的一笔钱的时间离现在越远，其现值就越低。
2．利息率越高，在未来某个特定时期被付给或收到的任意一笔钱的现值就越低。
表B2．1未来1美元的现值
______________________________________________
年份 3％ 4％
5％ 6％ 8％ 10％ 20％
年份
1 ．971 ．962
．952 ．943 ．926 ．909 ．833 1
2 ．943 ．925
．907 ．890 ．857 .
826 ．694 2
3 ．915 ．890
．864 ．839 ．794 ．751 ．578 3
4 ．889 ．855
．823 ．792 ．735 ．683 ．482 4
5 ．863 ．823
．784 ．747 ．681 ．620 ．402 5
6 ．838 ．790
．746 ．705 ．630 ．564 ．335 6
7 ．813 ．760
．711 ．665 ．583 ．513 ．279 7
8 ．789 ．731
．677 ．627 ．540 ．466 ．233 8
9 ．766 ．703
．645 ．591 ．500 ．424 ．194 9
10 ．744 ．676 ．614 . 558
．463 ．385 ．182 10
11 ．722 ．650 ．585
．526 ．429 ．350 ．134 11
12 ．701 ．625 ．557
．497 ．397 ．318 ．112 12
13 ．681 ．601 ．530
．468 ．368 ．289 ．0935 13
14 ．661 ．577 ．505
．442 ．340 ．263 ．0779 14
15 ．642 ．555 ．481
．417 ．315 ．239 ．0649 15
16 ．623 ．534 ．458
．393 ．292 ．217 ．0541 16
17 ．605 . 513 ．436
．371 ．270
．197 ．0451 17
18 ．587 ．494 ．416
．350 ．250 ．179 ．0376 18
19 ．570 ．475 ．396
．330 ．232 ．163 ．0313 19
20 ．554 ．456 . 377
．511 ．215 ．148 ．0261 20
25 ．478 ．375 ．295
．232 . 146 ．0923 ．0105 25
30 ．412 ．308 ．231
．174 ．0994 ．0573 ．00421 30
40 ．307 ．208 ．142
．0972 ．0460 ．0221 ．000680 40
50 ．228 ．141 ．087
．0543 ．0213 ．00852 ．000109 50
________________________________________________
上表每一行表示未来一定年份结束时可得到的钱现在值多少，例如，年利五厘，20年后的1美元现在只值37．7美分，第50年未，它一角钱也不值，要知道从现在起一定年份后的10000美元现在值多少，只要用该行的数字乘10000就行了。例如，以贴现率为5％算，第10年年未所得10000美元现在只值6140美元。
每年得到的一笔固定收入的现值（一组未来定期数额的序列）我们可用上述现值公式来推算某预期未来收入流量的现值（也称资本化值和贴现值）。例如，在一种最简单情形下，我们想要知道的是未来的20年中每年有1美元固定收入的现值或资本化值。我们将要考察的是未来支付的款项的流量。我们需要得到的那笔钱现在必须放在一边，并以某个特定利率生息。这笔钱将在所需时期中按期支付一定金额，直到最后支付的那笔钱恰好把最初的款项用完为止。为了找出这个未知数额，即现值，我们必须贴现未来每年得到的1美元。可以运用以下公式来算，设A1是第1年末的所得1美元，A2是第2年末的所得1美元，A2o是第20年末的所得1美元：
（B2.7）
等式（B2.7）这一公式常称为资本值公式，而不称现值公式。它表明如果计算将来获得一系列收入（或担负一系列成本）的权利的当前价格。
若得到的收入或担负的成本流量永远流转下去，或者说趋于无穷，等式（B2.7）就简化为
P＝A/r
（B2.8）
这里A代表永久性年度所得或所花的一笔数额。为使该公式成立，每年这笔数额必须是固定不变的。该公式是对20年以上时期中的较高利率所得到的现值的一种近似计算。见表B2．2。在这里我们示意的是每年年末所得1美元固定收入的资本值现值。40年后现值极其接近于年份趋于无穷远时的现值——5美元．因此公式（B2.8）是一个很好的近似，尽管每1美元支付款项序列决不会是无限延续下去的。
这里我们表示了在一定年份中每一年末所得1美元的现值。例如，设年利5厘，10年小每一年年末所得1美元的现值便是7．72美元。若年份为50年，则所得1美元每年年末现值为18．30美元。
表B2.2
不同贴现率各时期1美无的现值
__________________________________________________
年份 3％
4％ 5％ 6％
8％ 10％
20％ 年份
1 0．971 0．960
0．952 0．943 0．926 0．909
0．833 1
2 1．91 1．89
1．86 1．83 1．78
1．73 1．53 2
3 2. 83 2．78
2．72 2．67 2．58
2．48 2．11 3
4 3. 72 3．63
3．55 3．46 3．31
31．6 2．59 4
5 4．58 4．45
4. 33 4．21 3．99
3．79 2．99 5
6 5．42 5．24
5．08 4. 91 4．62
4．35 3．33 6
7 6. 23 6．00
5．79 5．58 5．21
4．86 3．60 7
8 7. 02 6．73
6. 46 6．20 5．75
5．33 3．84 8
9 7．79 7．44
7．11 6. 80 6．25
5．75 4．03 9
10 8．53 8．11
7．72 7. 36 6．71
6．14 4．19 10
11 9．25 8．76
8．31 7. 88 7．14
6．49 4．33 11
12 9．95 9．39
8．36 8. 38 7．54
6．81 4．44 12
13 10. 6 9．99
9．39 8. 85 7．90
7．10 4．53 13
14 11．3 10．6
9．90 9．29 8．24
7．36 4．61 14
15 11．9 11．1
10．4 9．71 8．56
7．60 4．68 15
16 12．6 11．6
10. 8 10．1 8．85
7．82 4．73 16
17 13．2 12．2
11．3 10．4 9．12
8．02 4．77 17
18 13．8 12．7
11．7 10．8 9．37
8．20 4．81 18
19 14．3 13．1
12．1 11．1 9．60
8. 36 4．84 19
20 14．9 13．6
12．5 11．4 9．82
8．51 4．87 20
25 17．4 15．6
14．1 12．8 10．7
9．08 4．95 25
30 19．6 17．3
15．4 13．8 11. 3
9．43 4．98 30
40 23．1 19．8
17．2 15．0 11．9
9．78 5．00 40
50 25．7 21．5
18．3 15．8 12．2
9．91 5．00 50
∞ 33. 3 25．0
20．0 16．7 12．5
10．00 5．00 ∞
利润流量的现值
现在我们可以看出，如果t年后成本等于Ct，t年后收益等于Rt，利润等于x，则从第1年起到第n年利润流量的现值等于
（B2.9）
| 